| Numéro |
J. Phys. I France
Volume 1, Numéro 8, August 1991
|
|
|---|---|---|
| Page(s) | 1093 - 1108 | |
| DOI | https://doi.org/10.1051/jp1:1991193 | |
DOI: 10.1051/jp1:1991193
J. Phys. I France 1 (1991) 1093-1108
S.Ph.T., C.E.N. Saclay, 91191 Gif-sur-Yvette Cedex, France
![\begin{displaymath}\int \left [\prod_{i=1}^n \mu (x_i)\right]\left[\prod_{1\le j...
...}\vert x_j-x_k\vert^{\beta}\right] {\rm d}x_{m+1}...{\rm d}x_n,\end{displaymath}](/articles/jp1/abs/1991/08/jp1v1p1093/img1.gif)
is calculated for the three values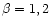 and 4, and integers
m and
n with
and 4, and integers
m and
n with
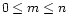 . For some applications one needs this integral when
. For some applications one needs this integral when
![$\mu(x)=\exp [-V(x)]$](/articles/jp1/abs/1991/08/jp1v1p1093/img4.gif) ,
V(x) an even polynomial, specially in the limit
,
V(x) an even polynomial, specially in the limit
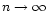 keeping
m finite. A conjecture for this limit in the case
keeping
m finite. A conjecture for this limit in the case
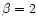 is given when
is given when
 .
.
© Les Editions de Physique 1991
J. Phys. I France 1 (1991) 1093-1108
A method of integration over matrix variables: IV
G. Mahoux and M.L. MehtaS.Ph.T., C.E.N. Saclay, 91191 Gif-sur-Yvette Cedex, France
(Received 1 February 1991, revised 7 April 1991, accepted 12 April 1991)
Abstract
The
m-point correlation function
![\begin{displaymath}\int \left [\prod_{i=1}^n \mu (x_i)\right]\left[\prod_{1\le j...
...}\vert x_j-x_k\vert^{\beta}\right] {\rm d}x_{m+1}...{\rm d}x_n,\end{displaymath}](/articles/jp1/abs/1991/08/jp1v1p1093/img1.gif)
is calculated for the three values
© Les Editions de Physique 1991



