| Numéro |
J. Phys. I France
Volume 6, Numéro 7, July 1996
|
|
|---|---|---|
| Page(s) | 907 - 923 | |
| DOI | https://doi.org/10.1051/jp1:1996106 | |
J. Phys. I France 6 (1996) 907-923
Dielectric Function and Interband Transitions in Hg
 Zn
Zn
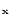 Te Solid Solutions
Te Solid Solutions
O. Castaing1, J.T. Benhlal1, R. Granger1 and R. Triboulet2
1 Laboratoire de Physique des Solides ERS F0134 CNRS, I.N.S.A, 35043 Rennes Cedex, France
2 Laboratoire de Physique des Solides LP 1332 CNRS, 1 place A. Briand 92195 Meudon Cedex, France
(Received 20 December 1996, received in final form 25 March 1996, accepted 9 April 1996)
Abstract
The dielectric function
![]() in Hg
1-xZn
x Te is found, for the first time, at 293 K. It is deduced from spectroscopic ellipsometry measurements for the entire composition
range and for photon energies ranging from 0.75 eV to 5.7 eV. A detailed analysis of the chemical treatments leading to the
best surfaces which correspond to the highest values of
in Hg
1-xZn
x Te is found, for the first time, at 293 K. It is deduced from spectroscopic ellipsometry measurements for the entire composition
range and for photon energies ranging from 0.75 eV to 5.7 eV. A detailed analysis of the chemical treatments leading to the
best surfaces which correspond to the highest values of
![]() at the
E2 peak is presented. The oxydation of the surface after the last stripping is also studied. The pseudodielectric function is
analysed for the critical point model. The variation, with
x of the parameters describing the main critical transitions
at the
E2 peak is presented. The oxydation of the surface after the last stripping is also studied. The pseudodielectric function is
analysed for the critical point model. The variation, with
x of the parameters describing the main critical transitions
![]() and
E2 are obtained. The results are discussed in relation to the band structure and to the properties of these compounds.
and
E2 are obtained. The results are discussed in relation to the band structure and to the properties of these compounds.
Résumé
La fonction diélectrique
![]() des solutions solides Hg
1-xZn
xTe est donnée, pour la première fois, à 293 K. Ces résultats sont déduits de mesures d'ellipsométrie spectroscopique dans
tout le domaine de composition et pour des énergies de photon allant de 0,75 eV à 5,7 eV. Les traitements chimiques permettant
d'obtenir les meilleures surfaces correspondant aux plus fortes valeurs de
des solutions solides Hg
1-xZn
xTe est donnée, pour la première fois, à 293 K. Ces résultats sont déduits de mesures d'ellipsométrie spectroscopique dans
tout le domaine de composition et pour des énergies de photon allant de 0,75 eV à 5,7 eV. Les traitements chimiques permettant
d'obtenir les meilleures surfaces correspondant aux plus fortes valeurs de
![]() au pic
E2 sont analysés en détail. De même, l'oxydation de la surface est suivie par ellipsométrie. La fonction pseudodiélectrique
est analysée avec le modèle de points critiques. Les variations des paramètres définissant les principales transitions
au pic
E2 sont analysés en détail. De même, l'oxydation de la surface est suivie par ellipsométrie. La fonction pseudodiélectrique
est analysée avec le modèle de points critiques. Les variations des paramètres définissant les principales transitions
![]() et
E2 sont données en fonction de la composition
x. Ces résultats sont discutés en relation avec la structure de bande et les propriétés de ces solutions solides.
et
E2 sont données en fonction de la composition
x. Ces résultats sont discutés en relation avec la structure de bande et les propriétés de ces solutions solides.
© Les Editions de Physiques 1996



