| Issue |
J. Phys. I France
Volume 6, Number 5, May 1996
|
|
|---|---|---|
| Page(s) | 641 - 648 | |
| DOI | https://doi.org/10.1051/jp1:1996234 | |
J. Phys. I France 6 (1996) 641-648
Random Magnetic Impurities and the
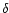Impurity Problem
Jean Desbois, Cyril Furtlehner and Stéphane Ouvry Division de Physique Théorique Unité de Recherche des Universités Paris 11 et Paris 6 associée au CNRS, IPN, Université Paris Sud, Bât. 100, 91406 Orsay Cedex, France
(Received 17 November 1995, received in final form 10 January 1996, accepted 22 January 1996)
Abstract
One considers the effect of disorder on the 2-dimensional density of states of an electron of charge
e in a constant magnetic field superposed onto a Poissonnian random distribution of point vortices carrying a flux
is the dimensionless coupling constant). If the electron Hilbert space is restricted to the Lowest Landau Level (LLL) of
the total average magnetic field, the random magnetic impurity problem is mapped onto a contact
impurity problem. Particular features of the average density of states are then interpreted in terms of the microscopic eigenstates
of the
N impurity Hamiltonian. The deformation of the density of states with respect to the density of impurities manifests itself
by the progressive depopulation of the LLL. A Brownian motion analysis of the model, based on Brownian probability distributions
for arithmetic area winding sectors, is also proposed. In the case
, the depletion of states at the bottom of the spectrum is materialized by a Lifschitz tail in the average density of states.
© Les Editions de Physique 1996