| Issue |
J. Phys. I France
Volume 7, Number 11, November 1997
|
|
|---|---|---|
| Page(s) | 1455 - 1473 | |
| DOI | https://doi.org/10.1051/jp1:1997141 | |
DOI: 10.1051/jp1:1997141
J. Phys. I France 7 (1997) 1455-1473
Département de Recherche Fondamentale sur la Matière Condensée, CEA Grenoble, 38054 Grenoble Cedex 9, France
(Received 17 February 1997, revised 19 June 1997, accepted 27 June 1997)
 scales with the wavelength
scales with the wavelength
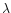 as
as
 for diffusion dynamics and as
for diffusion dynamics and as
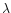 as
as
 for evaporation dynamics. In the case of evaporation dynamics, the transient profile is sinusoidal. In the case of surface
diffusion the profile presents blunted parts at the top and at the bottom, which result from the kinetic attraction between
steps.
for evaporation dynamics. In the case of evaporation dynamics, the transient profile is sinusoidal. In the case of surface
diffusion the profile presents blunted parts at the top and at the bottom, which result from the kinetic attraction between
steps.
© Les Editions de Physique 1997
J. Phys. I France 7 (1997) 1455-1473
Relaxatin of a Grooved Profile Cut in a Crystalline Surface of High Symmetry
Erwan Adam, Anna Chame, Frédéric Lançon and Jacques VillainDépartement de Recherche Fondamentale sur la Matière Condensée, CEA Grenoble, 38054 Grenoble Cedex 9, France
(Received 17 February 1997, revised 19 June 1997, accepted 27 June 1997)
Abstract
The smoothing of artificial grooves on a high-symmetry crystal surface below its roughening transition is investigated in
the light of a one-dimensional model. In the case of diffusion dynamics, a new, kinetic, attractive interaction between steps
opposes the contact repulsion and tends to flatten the top and the bottom of the profile in the transient state anterior to
complete smoothing. This phenomenon, which is absent from continuum models, is weaker, but still present in real, two-dimensional
surfaces.
© Les Editions de Physique 1997



